To understand the reason for a 1-bit Dual D/A converter, it is helpful to know a little about the digital-to-analog conversion process. In a CD (and any other digital recording technology), the goal is to create a recording with very high fidelity (very high similarity between the original signal and the reproduced signal) and perfect reproduction (the recording sounds the same every time you play it no matter how many times you play it). To accomplish these two goals, digital recording converts the analog wave into a stream of numbers and records the numbers instead of the wave. The conversion is done by a device called an analog-to-digital converter (ADC). Then, to play back the music, the stream of numbers is converted back to an analog wave by a digital-to-analog converter (DAC). The analog wave produced by the DAC is amplified and fed to the speakers to produce the sound.
When you sample the wave with an analog-to-digital converter you have control over 2 variables:
Advertisement
- Sampling rate - controls how many samples are taken per second
- Sampling precision - controls how many different gradations (quantization levels) are possible when taking the sample
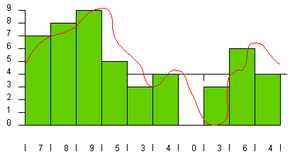
In the following figure, let's assume that the sampling rate is 1,000 per second and the sampling precision is 10:
The green rectangles represent samples. Every 1/1000th of a second, the ADC looks at the wave and picks the closest number between zero and 9. The number chosen is shown along the bottom of the figure above. These numbers are a digital representation of the original wave. When the DAC recreates the wave from these numbers, you get the blue line shown in the following figure:
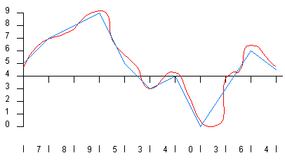
You can see that the blue line lost quite a bit of the detail originally found in the red line, which means the fidelity of the reproduced wave is not very good. This is the sampling error. You reduce sampling error by increasing both the sampling rate and the precision. In the following figure, both the rate and the precision have been improved by a factor of 2 (20 gradations at a rate of 2,000 samples per second):
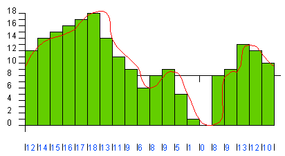
In the following figure, the rate and the precision have been doubled again (40 gradations at 4,000 samples per second):
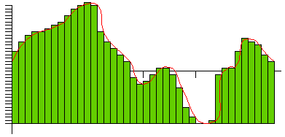
You can see that as the rate and precision improve, the fidelity (similarity between the original wave and the DAC's output) improves. In the case of CD sound, fidelity is an important goal, so the sampling rate is 44,100 samples per second (44.1 KHz) and the number of gradations is 65,536. At this level, the output of the DAC so closely matches the original wave form that the sound is essentially "perfect" to most human ears.
The DAC typically uses a different resistor for each bit. A 4-bit DAC needs 4 resistors working in parallel to provide a steady analog signal. When you get to the 16-bit or even 32-bit level found in CDs and DVDs, the number of gradations required per resistor makes it very difficult to precisely match values. For example, a typical 16-bit DAC would have 16 resistors requiring a total of 65,536 gradations.
What a 1-bit Dual D/A converter does is allow the digital-to-analog conversion to happen without the need for all those extra resistors. Essentially, this type of DAC does not use a bank of resistors operating in parallel. Instead, it creates a carefully modulated signal from the digital. The converter relies on noise shaping, a phenomenon that takes advantage of the human ear's inability to notice noise when it occurs in higher frequencies. Basically, the human ear is most sensitive to noise at 5 KHz, and is almost unable to detect it at 20 KHz.
A key part of the converter is a circuit called a delta-sigma modulator, which takes the binary signal (1s and 0s) from the CD and changes them to a steady pulse, called a pulse train. The pulse train contains an average of the change in the amount of energy represented in the sample. A low-pass filter removes all time-domain information and recovers only the average energy of the pulse train that feeds it. The key here is to understand that the pulse-train waveform is clocked at a very high frequency compared to the 44.1 KHz sample rate. The pulse train is sent through the DAC and changed into an analog signal.
The delta-sigma circuit has two main sections:
- Delta receives the incoming digital signal and monitors the outgoing pulse train. It creates an error signal, which is based on the difference between the binary signal coming in and the pulse train going out.
- Sigma adds up the results of the error signal created by delta and supplies this sum to the low-pass filter.
The error signal is used by the low-pass filter to average the analog signal. Basically, this means that minute adjustments are made to the analog signal to compensate for the differences between the binary signal and the pulse train. This page provides incredible detail and diagrams of the entire circuit, as well as a detailed explanation of the process.
Here are some interesting links:
Advertisement